Przygotowanie danych
Dane badawcze do analiz można opracowywać w różnych formatach. Schöch (2013) rozróżnia dane ustrukturyzowane (baza danych), częściowo ustrukturyzowane (XML) i nieustrukturyzowane (np. tekst). Struktura danych może zaś być linearna (np. tabelaryczna), hierarhiczna (np. drzewo) lub relacyjna (sieć). Najpopularniejszą obecnie formą przechowywania danych w humanistyce są tabele, które można edytować popularnymi programami biurowymi (np. Excel, OpenOffice Calc, Google spreadsheets) i eksportować do prostego pliku CSV, odczytywanego przez inne programy. W dalszych częściach spróbujemy zbudować próbną sieć. Publiczność zainteresowaną bardziej rozbudowanymi przykładami odsyłam do analizy Makbeta na podstawie relacji między osobami dramatu w poszczególnych scenach (ShakespeareMacbeth).
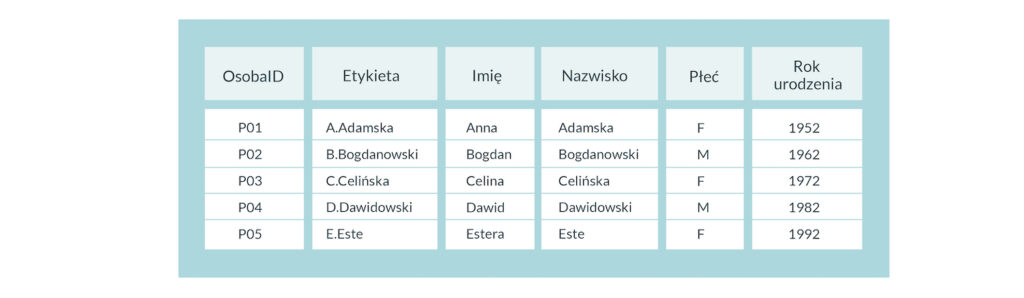
Dane dzielimy na kolumny, które opatrujemy nagłówkami (najlepiej bez spacji i polskich znaków), a w kolejnych wierszach podajemy kolejne obserwacje. Tab.1. zawiera przykładowe dane dotyczące postaci. Pierwsza kolumna zawiera unikalny identyfikator bytu (ważne, by trzymać się spójnej konwencji). Kolumna label to nazwa bytu do wyświetlania, zaś kolejne dane (imię, nazwisko, płeć, rok urodzenia). Zwróćmy uwagę, że dane mogą przyjmować różne wartości: ciąg znaków (imię i nazwisko), daty i liczby (rok urodzenia) czy kategoryzacja (płeć).
Tab. 1 Przykładowe dane tabelaryczne
W przypadku analizy sieciowej potrzebujemy zakodowania relacji między dwoma bytami –– relację nazywamy krawędzią (edge), byty zaś węzłami (node). Dodatkowo, sama relacja może mieć własne atrybuty, jak data czy waga (weight), która oznacza siłę relacji (np. jeśli dani autorzy A i B napisali wspólnie 2 teksty, a autorzy B i C, tylko jeden, to krawędź A-B może mieć wagę dwa, a B-C jeden).
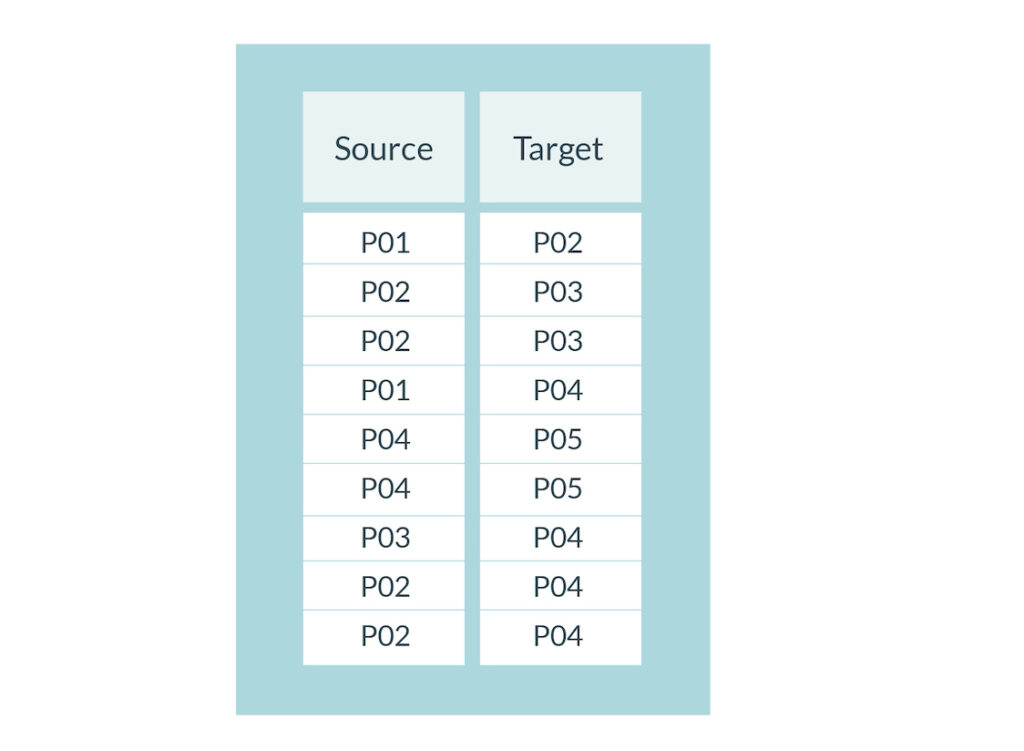
W naszym przykładzie kodujemy relacje między osobami z Tab.1 na podstawie jakiegoś zjawiska, które je łączy. Na przykład faktu cytowania jednej osoby przez drugą. W efekcie powstaje lista par osób wzajemnie się cytujących (Tab. 2). P01 cytuje P02 i P04, itd.
Tab. 2 Przykładowe relacje między bytami
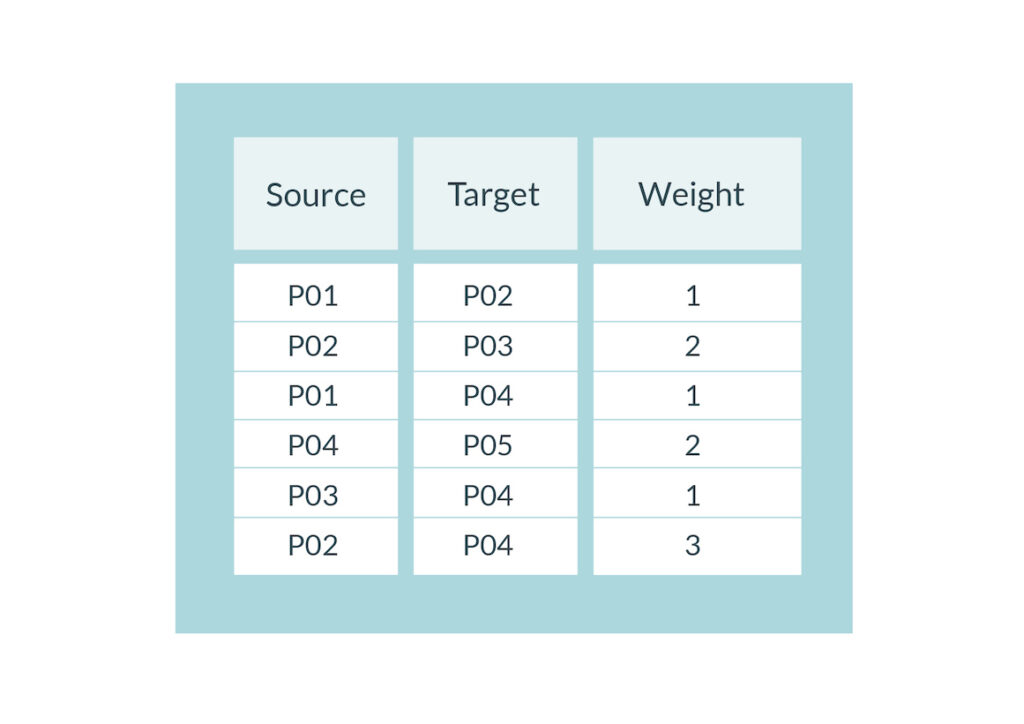
Możemy tę listę dodatkowo uprościć, przekształcając powtarzające się pary na krawędzie o różnej wadze. Jeżeli osoba cytowała drugą tylko raz, waga będzie na poziomie jeden, jeżeli dwukrotnie – dwa, trzykrotnie – trzy i tak dalej (Tab. 3).
Tab. 3 Uporządkowana tabela krawędzi z wagami
Tak przygotowane dane można już wprowadzać do analizy do popularnych programów grafowych (np. omawianego niżej GEPHI). Dodajmy, że na etapie przygotowywania i wprowadzania danych ustalamy też, czy relacja jest skierowana i – jeśli tak – jaki ma kierunek. W naszym przykładzie mamy do czynienia z relacją skierowaną (A – cytuje → B). Oczywiście od przyjętej przez nas metodologii zależy, jaki kierunek ustanowimy – możemy równie dobrze uznać, że (B – jest cytowany przez → A). Ważne, by trzymać się tych zasad konsekwentnie.
Relacja nieskierowana, dla odmiany, zakłada pewną równoważność –– jak współwystępowanie. Gdyby nasze dane przedstawiały nie tyle relacje cytowań, ile współautorstwo artykułów naukowych, to mielibyśmy relację nieskierowaną (B ← jest współautorką → A). Ta różnica jest bardzo istotna, ponieważ niektóre statystyki sieci zależą od tego czy graf jest skierowany czy nie. W przypadku GEPHI podejmujemy tę decyzję dla całego grafu, wprowadzając dane. W przypadku baz grafowych jak Neo4j możemy pracować na różnorodnych relacjach.
Sieci mono- i wielomodalne
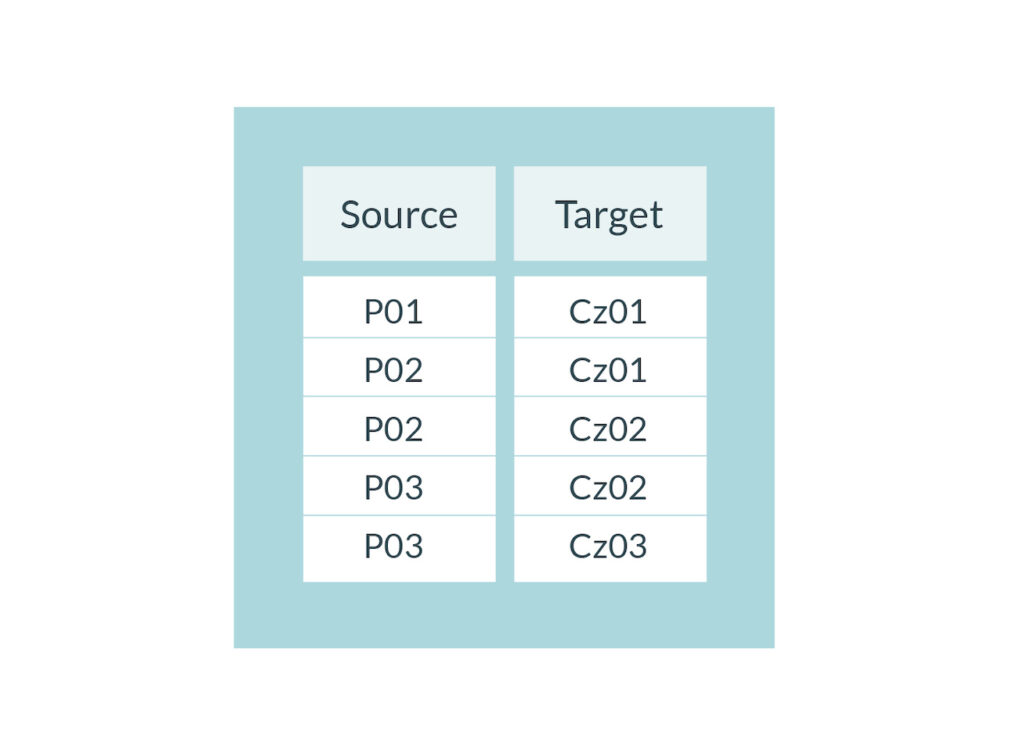
Wreszcie, warto pamiętać, że większość algorytmów w dostępnych programach do analizy sieciowej jest oparta na założeniu o monomodalności sieci, tzn. że wszystkie elementy mogą się potencjalnie ze sobą łączyć. Sieć budowana na omawianych wyżej relacjach spełnia ten warunek, ponieważ występuje jeden typ bytu – osoba – który potencjalnie może wejść w relację cytowania ze wszystkimi pozostałymi bytami. Sprawa się skomplikuje, gdybyśmy wprowadzimy nowy typ bytu – np. czasopismo. Spójrzmy na Tab.4, która zawiera dane na tematy trzech osób (P) publikujących w trzech czasopismach (Cz). Jako że mamy tu dwa typy bytów, taką sieć określamy mianem bimodalnej (możliwe są też sieci wielomodalne z kolejnymi typami bytów, jak np. wydawcy, książki, nagrody). Zwróćmy jednak uwagę, że w tej sieci nie mamy swobody zawiązywania relacji między wszystkimi elementami (nie ma relacji P-P albo Cz-Cz).
Tab. 4 Relacje w sieci bimodalnej
I choć można taką sieć analizować w bazach grafowych, to algorytmy takich narzędzi jak Gephi działają na założeniu o monomodalności, np. przy wyliczaniu liczby możliwych połączeń w sieci. Dlatego też, by zastosować algorytmy dla tych sieci, musimy dokonać projekcji monomodalnej, czyli przekształcić relacje między różnymi typami na relację między tym samym typem. A zatem, w naszym przykładzie, w zależności od pytania badawczego, możemy wybrać, czy przekształcamy naszą sieć osób publikujących w czasopismach na sieć relacji między osobami (publikowanie w tym samym czasopiśmie tworzy krawędź między dwoma osobami), czy czasopismami (jeżeli jedna osoba publikowała w dwóch czasopismach, tworzymy krawędź między nimi) (Tab.5).
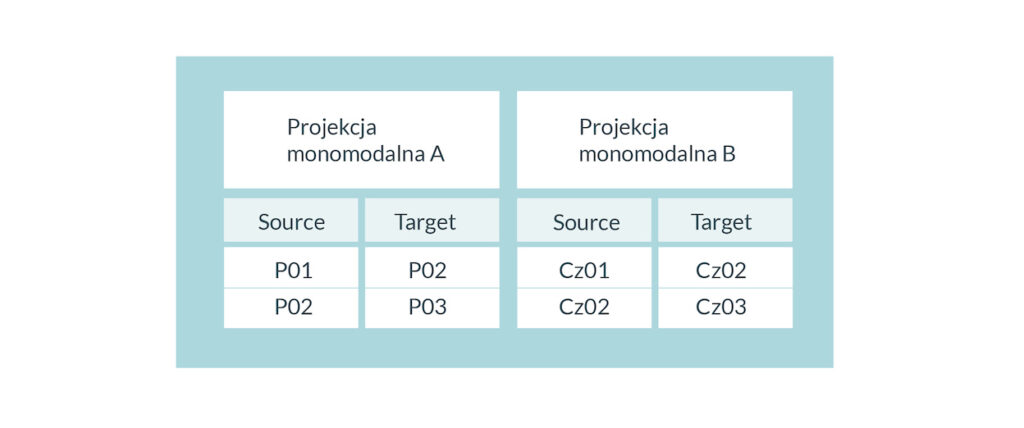
Tab. 5 Przykład projekcji monomodalnej. Wariant A – relacje między autor(k)ami. Wariant B – relacje między czasopismami
